【3分でわかる算数】ケーニヒスベルクの七つの橋問題~一筆書の成立条件~

算数

2021.01.05 2021.01.04

人気の無い3分でわかる算数シリーズ。今回は筆者が栄光学園コースの授業で解いた問題。天才どもがこの話を知っていて衝撃を受けたのを思い出したので記事にしました。数学大好きな保護者の方なら一度は受験生に話したことがあるかもしれません。

問題

http://www.taxlabo.com/it_kenbunroku/dai_6wa.html

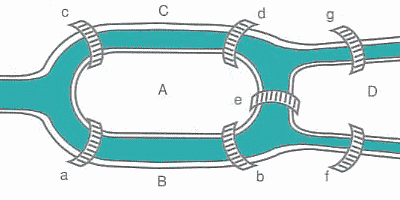
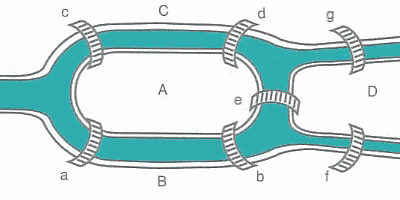
18世紀初頭,ケーニヒスベルク(現在のカリーニングラード)には7つの橋があった。住人たちは画像の範囲内で橋を二回以上渡らず、すべての橋を渡ることは出来るのかについて議論していた。住人の一人となって渡ることができるならその方法を、出来ないならその理由を答えてください。

まず初めに、結局渡ることはできないです。そしてその理由説明は知らなければ世紀の天才でもない限り絶対にできません。だから解けなくても安心して下さい。理由を知っていた対策コースの連中があたまおかしいだけだから…。

さて、先ほどの橋の図、橋を線で表すように書きなおすと、

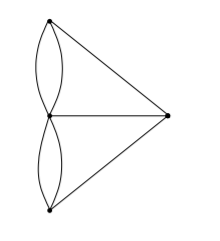
こんな感じに書き直せます。この図は頂点を地面、線を橋とみなすことで書けます。で、橋を一度に渡れるか＝この図を一筆書きできるかという問題に置き換えることができるわけです。さて、ここである定理を紹介させていただきます。

図のような線と点で構成されたものをグラフと呼ぶ。グラフの

点:頂点

線:辺

点につながる線の数:次数

と呼ぶことにする。この時

1.すべての頂点の次数は偶数である。

2.2つの頂点の次数が奇数でその他のすべての頂点の次数は偶数である。

の二つのうち少なくともどちらか一方の条件が成立する状況下でのみ一筆書きを行うことができる。

今回の問題はオイラーがこの定理を生み出すことで結論が出たわけです。さて、この定理に従って図の次数をチェックすると、

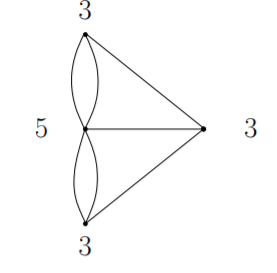
どちらも満たしてないですね。ということで一筆書きは出来ないという結論が出せます。初見ならオイラークラスの天才でもない限り絶対解けません。ちなみにこの定理からトポロジーという学問が生まれました。

「算数」であるため定理の証明は控えておりますが、もっと詳しく知りたいのであれば

この公開されていたPDFがいいかなと思います。最も小学生には厳しすぎる(前提知識不足的な意味で)と思うので保護者の方が読んで噛み砕いた物を伝えることを推奨しますが…。

この定理は塾で習うことは無い(対策コース等特別な状況下を除いて)と思います。しかし一部のいかれた連中は知っていた。常日頃から受験のみならず様々なことに積極的に触れていることが彼らを天才にしたのでしょう…。